排序的介绍

排序指的就是将一组无序的数据按特定规则(升序或降序)重新排列为有序序列的过程。

l 按是否占用额外空间分类

内部排序：待排序的数据在内存中完成排序。

外部排序：带排序的数据量极大，须借助外部存储设备存放。

l 按排序的稳定性分类

稳定排序：相同元素的相对位置在排序后保持不变

不稳定排序：相同元素的相对位置在排序后可能改变

插入排序

介绍

可以把插入排序的过程想象成摸取扑克牌排顺序的的过程，当摸第一张扑克牌在手上时，那就默认这张牌是排好序的，再摸一张时，就把摸到的这一张牌和手上的那一张作比较，然后按扑克牌大小的顺序把摸到的这张放到手上这张的左边或右边。接着在摸一张，将摸到的牌和手上的两张牌分别作比较(不一定比较两次)，然后将摸到的牌放到正确的地方，比如插到两张牌的中间。这个过程有一个规律，那就是手上拿的牌始终是排好序的，当再摸到一张牌时，将它和手上的每一张牌做对比，然后插入到合适的地方来使手中的牌有序。

实现

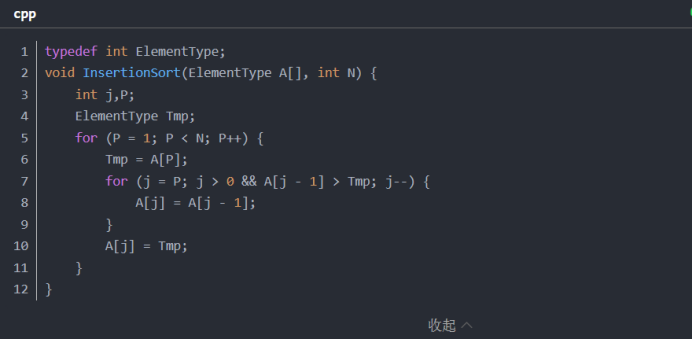
首先对于任何一个算法都需要待排序的数组A[]和待排序元素的数量N，j和P是用来遍历的，tmp是临时存储正在进行排序的那个元素。这里再补充一句，由于数组本身就是一个指针，所以这个排序函数的参数就是一个数组，这同时意味着只要在函数中将数组排好序了，那调用这个函数的地方的数组也就排好序了。

首先把整个数组的第一个元素当作是有序的，然后将第二个元素(下标为1)先用Tmp保存，接着遍历这个待比较元素前面的所有元素，我们要做的就是把这个待比较元素插入到前面有序序列中最大的小于这个待比较元素的元素的后面，在这个过程中，那些有序序列中所有比待比较元素大的元素就要统统后移。具体的实现就是通过第二个for循环让A[j]<A[j-1]实现的，以下是步骤的配图：

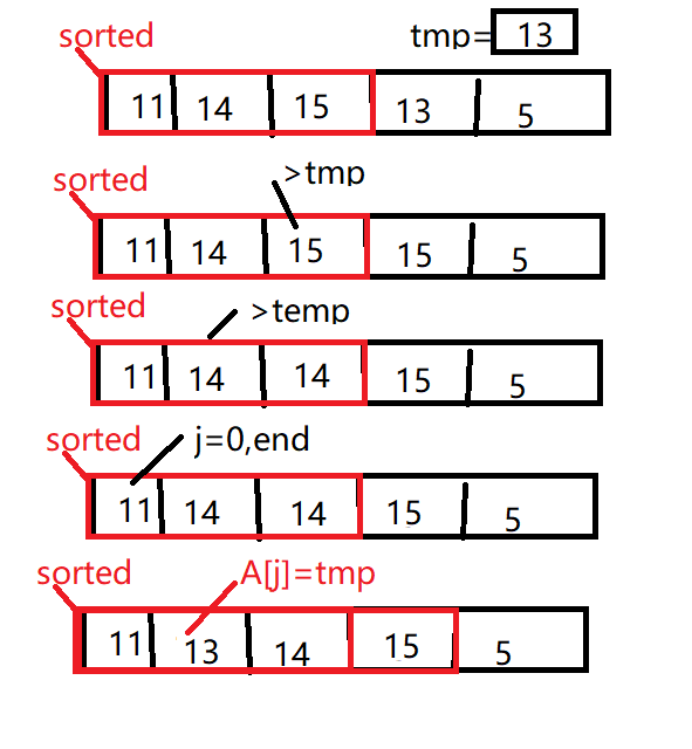
分析

        首先分析其时间复杂度：代码中第一个for循环表示要进行N-1次的插入排序，因为我们默认序列中的第一个元素是有序的，所以要对剩下的N-1的元素进行插入排序。对于每一个要进行插入排序的元素，在最坏的情况要和已排好序的序列元素都进行对比。这也对于第二个for循环，假设由N个元素，第2个元素要对比1次，第3个元素最坏要对比2次，第N个元素最坏要对比N-1次。累计求和会发现其时间复杂度就是O().

而对于每一次的插入排序，都是把那个插入的元素放到‘最好的位置’，在没插入之前的这个元素所在的位置，其前面大概率由多个大于它的元素，而插入之后的位置，其前面就没有大于它的元素了，所以我们可以说每一次插入都消除了这个元素的所有逆序数，也就是说一次插入操作可消除多个逆序。

冒泡排序

介绍

沸水沸腾时如果观察的话就能发现由于水压的影响，小气泡在上升过程的体积会逐渐增大，也就是说最大的气泡在水的最上面。冒泡排序的逻辑就是进行多次的相邻元素的两两比较，将最大的元素逐个放到序列的最后位置。

实现

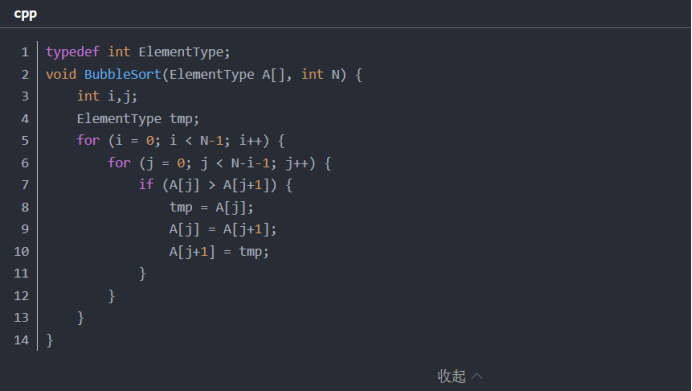
逻辑是，有N个元素构成的无序数组，逐次对每两个相邻元素进行对比在消逆序，每轮冒泡排序后总能把最大的元素排到数组的最后最后，这样最大的元素就归位了，其元素就不会在移动位置了，当进行N-1轮排序后，就有N-1个元素归位了，那剩下的那个元素就自动归位了，所以只需进行N-1轮排序即可。这样第一个for循环的终止条件就是i<N-1了。

接下来分别得到数组第一个位置和第N-i-1的位置(就是数组后排序顺序的最左边的位置的前第2个位置)，然后依次对每一个位置让它和它相邻后面的位置的元素进行比较和交换操作。这样就每一轮都会把数组前面乱序中的最大元素移到乱序的最后位置。

分析

首先看比较的次数，一共N-1轮，第一轮最坏要比较N-1次，第二轮要比较N-2次，第N-1轮要比较1次，累加后的时间复杂度依然是O()。

冒泡排序中每一趟可消除一个元素的所有逆序数，每一次交换可消除一共逆序数。

冒泡排序是稳定的，因为当前一个元素大于后一个元素时才会交换，俩元素相等并不会触发交换操作。